树链剖分

发表于 | 分类于 ，

闲来无事, 研究了一下这个神奇却又不算复杂的东西

什么是树链剖分:

顾名思义, 树链剖分就是把一棵树剖成一条条的树链, 再将树链存储为区间, 但实际操作中通常把所有的树链用一个区间存储

剖分的方法有几种, 但用得多的还是重链剖分

重链剖分指的就是把某个结点与它的重儿子(子树大小最大的子结点)编成一条链

实现:

重链剖分是基于dfs的, 所以也可以称之为一种”启发式的dfs序”

重链剖分一般用两个dfs实现:

第一遍dfs: 计算子树大小, 寻找重儿子

伪代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
int dep[Mn],size[Mn],hs[Mn],fa[Mn];	//结点深度,结点子树大小,结点的重儿子,父结点
void dfs1(int p)
{
    size[p] = 1;
    for(x=child of p)
    {
        dep[x] = dep[p]+1;
        fa[x] = p;
        dfs1(x);
        size[p] += size[x];
        if(size[x]>size[hs[p]])	hs[p] = x;
    }
}

第二遍dfs(重点部分): 记录每个结点的时间戳, 把重儿子拉成链, 记录每个结点所在链的链顶(即同一条链上深度最小的结点)

伪代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int tp[Mn],a[Mn],visit_c[Mn],dfs_c(0); //链顶,dfs序,访问时间,计数器
void dfs2(int p)
{
    a[++dfs_c] = p;
    visit_c[p] = dfs_c;
    if(hs[p])	//如果重儿子存在(非叶子结点)
    {
        tp[hs[p]] = tp[p];	//拉成重链
        dfs2(hs[p]);
    }
    for(x=child of p)
    {
        if(x!=hs[p])
        {
            tp[x] = x;
            dfs2(x);
        }
    }
}

树链剖分求LCA:

几乎所有树上问题都要求LCA, 所以求LCA是树链剖分的一项重要操作

树链剖分求LCA的方式略微有点像倍增LCA

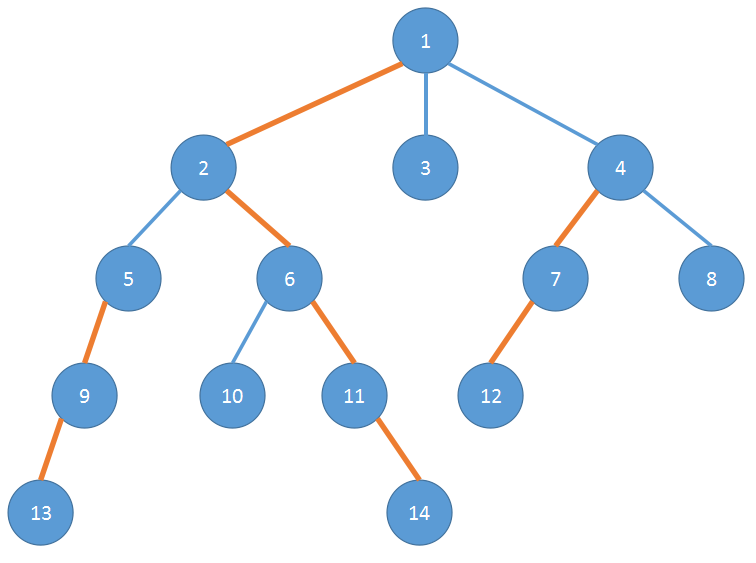
cutted tree

(橙色的边就是重链上的边)

方法就是如果两个结点不在同一条重链上时, 将链顶深度较大的那个结点跳到它所在的重链的链顶的父结点, 直到这两个结点在同一条重链上, 返回深度较小的那个结点

比如说要找这棵树的LCA(13,10)

d(13)>d(10), 所以首先将13跳到2

然后d(2)<d(10), 将10跳到6

此时2和6在同一条重链, 返回深度较小的结点, 所以LCA(13,10)=2

这里有个重要的定理, 是关于树链剖分的时间复杂度的:

若v是u的子结点, 且(u,v)是轻边(不在重链上的边), 则有size(v)<size(u)/2

理由很简单, 如果size(v)>=size(u)/2的话, 那么size(v)将会比u的任何一个儿子的size都要大, (u,v)就是重边(即在重链上的边)了

由此可得一个推论: 对于任意一个非根节点u, 在u到根节点的路径上, 轻边和重链的条数不超过log2n, 因为每经过一条轻边size都会减半(可以把这里的size看作可行范围)

所以, 树链剖分LCA的时间复杂度是O(log2n), 因为每个非根链顶与其父亲之间的边都是轻边

应用:

搞定树链剖分就可以在大多数树上问题上为所欲为啦~

只需要在求LCA的过程中顺便维护重链区间就好了

放几道例题来感受一下: