Miscellaneous of Fourier Transform

发表于 2022-11-16 分类于 note ， misc

傅里叶级数

傅里叶认为，对于周期为 $2\pi$ 的函数，均可展开为如下的级数形式:

\[ f(x) = \frac{a_0}{2} + \sum_{i=1}^{\infty}(a_i\cos ix + b_i\sin ix) \]

系数 $a_0, a_i, b_i$ 称为傅里叶系数.

由于三角函数系具有正交性，即:

\[\begin{aligned} \int_{-\pi}^{\pi} \cos nx\ {\rm d}x &= 0\ (n \in \mathbb{N}^+) \\ \int_{-\pi}^{\pi} \sin nx\ {\rm d}x &= 0\ (n \in \mathbb{N}^+) \\ \int_{-\pi}^{\pi} \sin nx \cos mx\ {\rm d}x &= 0\ (n,m \in \mathbb{N}^+) \\ \int_{-\pi}^{\pi} \sin nx \sin mx\ {\rm d}x &= 0\ (n,m \in \mathbb{N}^+, n \ne m) \\ \int_{-\pi}^{\pi} \cos nx \cos mx\ {\rm d}x &= 0\ (n,m \in \mathbb{N}^+, n \ne m) \\ \end{aligned}\]

上式可由定积分与积化和差公式证明.

同时有:

\[\begin{aligned} \int_{-\pi}^{\pi} 1\ {\rm d}x &= 2\pi \\ \int_{-\pi}^{\pi} \cos^2 nx\ {\rm d}x &= \pi\ (n \in \mathbb{N}^+) \\ \int_{-\pi}^{\pi} \sin^2 nx\ {\rm d}x &= \pi\ (n \in \mathbb{N}^+) \\ \end{aligned}\]

所以可得 (需满足一致收敛):

\[\begin{aligned} a_0 &= \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)\ {\rm d}x \\ a_n &= \frac{1}{\pi} \int_{-\pi}^{\pi}f(x)\cos nx\ {\rm d}x\ (n \in \mathbb{N}^+) \\ b_n &= \frac{1}{\pi} \int_{-\pi}^{\pi}f(x)\sin nx\ {\rm d}x\ (n \in \mathbb{N}^+) \\ \end{aligned}\]

若 $f(x)$ 为奇函数，$a_n$ 均为 0, 此时傅里叶级数为正弦级数；同理，若 $f(x)$ 为偶函数傅里叶级数为余弦级数.

由欧拉公式 ($\rm j$ 为虚数单位):

$$ e^{{\rm j}x} = \cos x + {\rm j}\sin x $$

可将傅里叶级数扩展至复数域:

$$\begin{aligned} f(x) &= \frac{a_0}{2} + \sum_{i=1}^{\infty}(a_i\cos ix + b_i\sin ix) \\ &= \frac{a_0}{2} + \sum_{i=1}^{\infty}(a_i\frac{e^{{\rm j}ix} + e^{-{\rm j}ix}}{2} - b_i{\rm j}\frac{e^{{\rm j}ix} - e^{-{\rm j}ix}}{2}) \\ &= \sum_{i=-\infty}^{+\infty} c_ie^{{\rm j}ix} \end{aligned}$$

其中:

\[\begin{aligned} c_0 &= \frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)\ {\rm d}x \\ c_n &= \frac{a_n - b_n{\rm j}}{2}\ (n \in \mathbb{N}^+) \\ c_{-n} &= \frac{a_n + b_n{\rm j}}{2}\ (n \in \mathbb{N}^+) \end{aligned}\]

三式合并即得:

\[ c_n = \frac{1}{2\pi} \int_{-\pi}^{\pi} f(x)e^{-{\rm j}nx}\ {\rm d}x \]

对于傅里叶级数，有帕塞瓦尔定理:

\[\begin{aligned} & \int_{-\pi}^{\pi} |f(x)|^2dx \\ =& 2\pi \left(\frac{a_0^2}{4}+\frac{1}{2}\sum_{i=1}^{\infty}(a_i^2 + b_i^2)\right) \\ =& 2\pi\sum_{i=-\infty}^{+\infty}|c_i|^2 \end{aligned}\]

使用三角函数系的正交性即可得证.

傅里叶变换

当周期不为 $2\pi$ 时，设周期为 $T$, 则有:

$$ f(x) = \sum_{i=-\infty}^{+\infty} c_ie^{{\rm j}\frac{2\pi ix}{T}} \\ c_i = \frac{1}{T}\int_{-T/2}^{T/2}f(x)e^{-{\rm j}\frac{2\pi ix}{T}}\ {\rm d}x $$

设 $\omega_i = 2\pi i/T$, 令 $F(\omega)=\alpha\displaystyle\int_{-T/2}^{T/2}f(x)e^{-{\rm j}\omega x} {\rm d}x$, 则:

$$ c_i = \frac{1}{T\alpha}F(\omega_i) \\ f(x) = \frac{1}{2\pi\alpha} \sum_{i=-\infty}^{+\infty} F(\omega_i)e^{{\rm j}\omega_i x} \frac{2\pi}{T} $$

当 $T \to +\infty$ 时，$f(x)$ 变为非周期函数，级数变为黎曼和，则有:

$$ F(\omega) = \alpha\int_{-\infty}^{+\infty}f(x)e^{-{\rm j}\omega x}\ {\rm d}x \tag{1} $$ $$ f(x) = \frac{1}{2\pi\alpha}\int_{-\infty}^{+\infty}F(\omega)e^{{\rm j}\omega x}\ {\rm d}\omega \tag{2} $$

式 $(1)$ 即为傅里叶变换，式 $(2)$ 为逆变换，一般视为算子将其记作 $FT[f(x)]$ 与 $IFT[F(\omega)]$. $\alpha$ 称为规范化因子，通常取为 $1$, 有时会取 $\frac{1}{ \sqrt{2\pi} }$

需要注意的是式中的 $\int_{-\infty}^{+\infty}$ 均为柯西主值积分，也即 $\lim \limits_{M\to +\infty}\int_{-M}^M$ 的缩写

与傅里叶级数同理，若 $f(x)$ 为奇函数则变换后为纯虚函数，若 $f(x)$ 为偶函数则变换后为实函数，分别称为正弦变换与余弦变换.

对于傅里叶变换，有线性性质:

\[ FT[af+bg] = aFT[f]+bFT[g] \]

频移特性与时移特性:

\[ FT[f](\omega + \omega_0) = FT[fe^{-{\rm j}\omega_0 x}](\omega) \\ FT[f(x+x_0)](\omega) = (e^{ {\rm j} \omega x_0}FT[f])(\omega) \]

比较重要的有时域卷积定理和频域卷积定理:

\[ FT[f*g] = FT[F] \cdot FT[g] \\ \frac{1}{2\pi}IFT[F*G] = IFT[F] \cdot IFT[G] \]

实数域 $\mathbb{R}$ 上的卷积定义如下:

\[ (f*g)(x) = \int_{-\infty}^{+\infty} f(t)g(x-t)\ {\rm d}t \]

若计算 $F(-\omega)$

\[\begin{aligned} F(-\omega) =& \int_{-\infty}^{+\infty}f(x)e^{ {\rm j}\omega x }{\rm d}x \\ =& \int_{-\infty}^{+\infty} f(x)\cos(\omega x) {\rm d}x \\ &+ {\rm j}\int_{-\infty}^{+\infty} f(x)\sin(\omega x){\rm d}x \\ =& \overline{F}(\omega) \end{aligned}\]

若函数为实函数则变换后的复函数实部为偶函数，虚部为奇函数. 负频率部分的幅值与正频率一致，相位角相反.

对于傅里叶变换也有帕塞瓦尔定理:

\[ \int_{-\infty}^{+\infty}|f(x)|^2{\rm d}x = \frac{1}{2\pi}\int_{-\infty}^{+\infty}|F (\omega)|^2 {\rm d}\omega \]

离散时间傅里叶变换

为了在计算机中表示信号，需要对连续的信号进行采样将其变为一个离散的数列.

为了对其进行分析，需要从数学上定义采样，为此首先需要引入冲激函数 (狄拉克 $\delta$ 函数), 它由两个式子定义:

\[ \begin{cases} \delta(x) = 0,\ x \neq 0 \\ \displaystyle\int_{-\infty}^{+\infty}\delta(x)\ {\rm d}x = 1 \end{cases} \]

也可定义为:

\[ \delta(x) = \frac{ {\rm d} u(x)}{ {\rm d} x }\\ u(x) = \begin{cases} 1&,x > 0 \\ 0&,x < 0 \end{cases} \]

$u(x)$ 为单位阶跃函数.

若函数 $f(t)$ 在 $t_0$ 处有值，显然有:

\[ f(t)\delta(t-t_0) = f(t_0)\delta(t-t_0) \]

同时显然 $\delta$ 函数为偶函数，所以:

\[\begin{aligned} \int_{-\infty}^{+\infty} f(t)\delta(x-t)\ {\rm d}t &= f(x)\int_{-\infty}^{+\infty}\delta(t-x)\ {\rm d}t \\ &= f(x) \end{aligned}\]

也即 $\delta$ 函数为卷积的单位元. 由时域卷积定理可以设 $FT[\delta] = 1$; 同时若对常函数 $1$ 进行 IFT, 则有:

\[IFT[1](x) = \frac{1}{2\pi}\int_{-\infty}^{+\infty}e^{ {\rm j} \omega x}\ {\rm d}\omega = \delta(x) \]

下面给出采样的数学定义。对于连续信号 $f(t)$, 对其进行采样即为:

\[ f^*(t) = f(t)\sum_{i=-\infty}^{+\infty}\delta(t-iT_s) \]

其中的 $T_s$ 称为采样间隔，一般记 $f_s=1/T_s$ 为采样频率，$\omega_s=2\pi f_s$ 为采样角频率.

若对 $f^*$ 进行傅里叶变换，则有:

\[\begin{aligned} FT[f^*](\omega) &= \int_{-\infty}^{+\infty} f(x)e^{-{\rm j}\omega x}\sum_{i=-\infty}^{+\infty}\delta(x-iT_s)\ {\rm d}x \\ &= \sum_{i=-\infty}^{+\infty}\int_{-\infty}^{+\infty} f(x)e^{-{\rm j}\omega x}\delta(x-iT_s)\ {\rm d}x \\ &= \sum_{i=-\infty}^{+\infty} f(iT_s)e^{-{\rm j} \omega iT_s} \end{aligned}\]

该变换即为离散时间傅里叶变换 (DTFT), 需要注意积分与求和的交换需要级数的一致收敛性.

DTFT 有一个重要性质。对 $s(t) = \sum_{i=-\infty}^{+\infty}\delta(t-iT_s)$ 求傅里叶级数:

\[\begin{aligned} c_n &= \frac{1}{T_s}\int_{-T_s/2}^{T_s/2} e^{-{\rm j} \omega_s nt} \delta(t)\ {\rm d}t \\ &= \frac{1}{T_s}\int_{-\infty}^{+\infty} e^{-{\rm j} \omega_s nt} \delta(t)\ {\rm d}t \\ &= \frac{1}{T_s} \end{aligned}\]

所以:

\[ s(t) = \frac{1}{T_s}\sum_{i=-\infty}^{+\infty}e^{ {\rm j} \omega_s it} \]

再对 $s(t)$ 进行傅里叶变换:

\[\begin{aligned} FT[s](\omega) &= \frac{1}{T_s}\int_{-\infty}^{+\infty} e^{-{\rm j} \omega t} \sum_{i=-\infty}^{+\infty}e^{ {\rm j} \omega_s it}\ {\rm d}t \\ &= \frac{1}{T_s} \sum_{i=-\infty}^{+\infty} \int_{-\infty}^{+\infty} e^{ {\rm j} (i\omega_s - \omega)t }\ {\rm d}t \\ &= \frac{2\pi}{T_s} \sum_{i=-\infty}^{+\infty} \delta(i\omega_s - \omega) \end{aligned}\]

对 $f^*$ 的傅里叶变换可以由频域卷积定理重新求得:

\[\begin{aligned} FT[f^*](\omega) &= \frac{1}{2\pi}(FT[f] * FT[s])(\omega) \\ &= \frac{1}{T_s} \int_{-\infty}^{+\infty}FT[f](\omega - u)\sum_{i=-\infty}^{+\infty} \delta(i\omega_s - u)\ {\rm d}u \\ &= \frac{1}{T_s} \sum_{i=-\infty}^{+\infty} \int_{-\infty}^{+\infty}FT[f](\omega - u) \delta(u - i\omega_s)\ {\rm d}u \\ &= \frac{1}{T_s} \sum_{i=-\infty}^{+\infty} FT[f](\omega - i\omega_s) \end{aligned}\]

也即在时域内以 $T_s$ 采样间隔进行采样，相当于在频域内以 $\omega_s$ 为周期进行周期延拓.

由此便有奈奎斯特采样定理: 若要保留 $\omega_N$ 以内的角频率信息，采样角频率要大于等于 $2\omega_N$, 否则将会发生频率混叠:

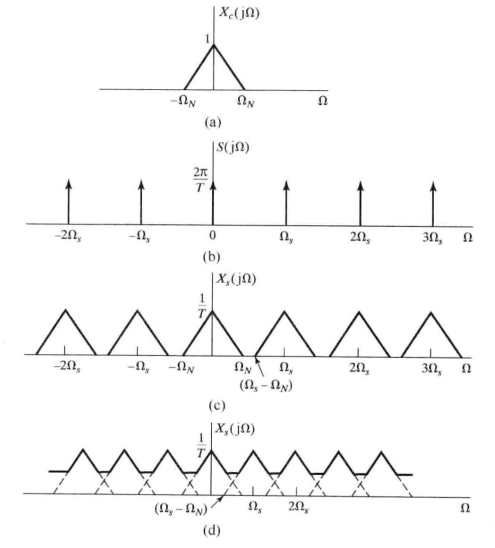
工程上由于后期处理的需求可能会略高于两倍，常用的音频采样率 44100Hz 便是由此而来 (人耳最多只能听到 20Hz-20kHz 的信息).

令 $x(n) = f(nT_s)$, 即频率归一化，则可将 DTFT 化简为:

\[X^*(\omega) = \sum_{n=-\infty}^{+\infty}x(n)e^{-{\rm j} \omega n}\]

同理，有逆 DTFT:

\[x(n) = \frac{1}{2\pi} \int_{-\pi}^{\pi} X^*(\omega)e^{ {\rm j} \omega n }\ {\rm d} \omega\]

离散傅里叶变换

DTFT 解决了离散信号频率分析的问题，但仍有问题需要解决: 一方面变换为一个无限长的级数求和，另一方面得到的函数仍然是连续函数.

第一个问题很好解决，实际输入的信号都是有限长度的，可记为 $x_0, x_1, \cdots, x_{L-1}$, 其余部分均取为 0 即可.

对于另外一个问题，可以考虑对频域同样进行” 采样”, 即在一个周期的区间 $[0, 2\pi)$ 中只取 $N$ 个等间距的点计算.

设计算的第 $k$ 个频率为 $\omega_k = 2\pi k/N$, 记 $X_k=X^*(\omega_k)$, 则有:

\[ X_k = \sum_{n=0}^{L-1}x_ne^{-{\rm j} \omega_k n } \]

通常记 $w_N = e^{-{\rm j}2\pi /N }$, 也即:

\[ X_k = \sum_{n=0}^{L-1}x_nw_N^{kn} \]

现在问题是 $N$ 的取值。若 $N<L$ 则有:

\[\begin{aligned} X_k &= \sum_{n=0}^{N-1}x_nw_N^{kn} + \sum_{n=N}^{L-1}x_nw_N^{kn} \\ &= \sum_{n=0}^{N-1}x_nw_N^{kn} + \sum_{n=0}^{L-N-1}x_{n+N}w_N^{kn} \\ \end{aligned}\]

发生了时域混叠，所以 $N$ 的取值必须大于等于 $L$, 为了方便起见一般令 $N=L$, $N>L$ 时向时域序列填充 0 即可:

\[ X_k = \sum_{n=0}^{N-1} x_nw_N^{kn} \tag{3} \]

这便是离散傅里叶变换 (DFT), 类似地，有逆 DFT:

\[ x_n = \frac{1}{N}\sum_{k=0}^{N-1}X_kw_N^{-kn} \tag{4} \]

证明可见这里 (FFT)

若 $n \geq N$ 则所得即为 $x_{n \mod N}$, 相当于对原信号进行了周期延拓.

同样在离散卷积的意义下 DFT 有时域卷积定理与频域卷积定理. 同时可以看出 DFT 与 IDFT 实际上是特殊点的多项式求值.

若计算 $X_{N-k}$:

\[\begin{aligned} X_{N-k} &= \sum_{n=0}^{N-1} x_nw_N^{(N-k)n} \\ &= \sum_{n=0}^{N-1} x_nw_N^{-kn} \end{aligned}\]

当 $x_n$ 均为实数时其值为 $\overline{X_n}$, 也即 DFT 所得的序列是一个共轭对称序列.

若计算 $X_0$:

\[ X_0 = \sum_{n=0}^{N-1} x_n \]

为 $x_n$ 的累加和，一般称该值为直流分量.

对 DFT 也有帕塞瓦尔定理:

\[ \sum_{n=0}^{N-1}|x_n|^2 = \frac{1}{N}\sum_{k=0}^{N-1}|X_k|^2 \]

Bluestein 算法

普通的 FFT 只能得到长度为 2 的整数次幂的 DFT, 对于其它情况则需要使用 Bluestein 算法快速计算.

对序列 $x_0, x_1, \cdots, x_{N-1}$ 进行 DFT, 有:

\[\begin{aligned} X_k &= \sum_{n=0}^{N-1} x_nw_N^{kn} \\ &= \sum_{n=0}^{N-1} x_nw_N^{(-(k-n)^2+k^2+n^2)/2} \\ &= w_N^{k^2/2}\sum_{n=0}^{N-1} x_nw_N^{n^2/2}w_N^{-(k-n)^2/2} \\ &= w_{2N}^{k^2}\sum_{n=0}^{N-1} x_nw_{2N}^{n^2}w_{2N}^{-(k-n)^2} \\ \end{aligned}\]

可以发现后面的求和为一个卷积，使用 FFT 计算卷积即可。时间复杂度为 $O(N\log N)$, 常数大约是 FFT 的六倍.

IDFT 也同理可得:

\[\begin{aligned} x_n &= \frac{1}{N}\sum_{k=0}^{N-1}X_kw_N^{-kn} \\ &= \frac{1}{N}\sum_{k=0}^{N-1} X_kw_N^{((n-k)^2-k^2-n^2)/2} \\ &= \frac{1}{N}w_{2N}^{-n^2}\sum_{k=0}^{N-1} X_kw_{2N}^{-k^2}w_{2N}^{(n-k)^2} \\ \end{aligned}\]

若使用的是 NTT 则可能需要计算二次剩余，此时可以使用:

\[ kn = \frac{-(k-n)^{\underline{2} } + k^{\underline{2} } + (n+1)^{\underline{2} } }{2} \]

来拆解 $kn$, 可避免计算二次剩余.

离散余弦变换

DFT 得到的结果为复数，有时不方便解释. 此时便可引入离散余弦变换 (DCT).

如前文所述，当信号是偶函数时进行傅里叶变换得到的便是实函数，所以对原信号进行偶延拓后再进行 DFT 便得到了 DCT. 偶延拓的方法不同得到的 DCT 也不同，其中最常用的一种如下:

\[\begin{aligned} y_k = 2\alpha_k \sum_{n=0}^{N-1} x_n \cos\left( \frac{\pi k(2n+1)}{2N} \right) \\ x_n = \frac{y_0}{2N\alpha_0} + \frac{1}{N} \sum_{k=1}^{N-1}\frac{y_k}{\alpha_k}\cos\left( \frac{\pi k(2n+1)}{2N} \right) \end{aligned}\]

相当于将信号右移 $1/2$ 个单位后进行偶延拓再进行 DCT. $\alpha_k$ 通常取 $1$, 有时为了使转移矩阵正交化会取为:

\[ \alpha_k = \begin{cases} \sqrt{\frac{1}{4N}},\ k=0 \\ \sqrt{\frac{1}{2N}},\ k>0 \end{cases} \]

DCT 可以更好的聚集低频能量 (由于进行了偶延拓后再周期延拓相比于 DFT 直接周期延拓函数图像更加平滑，高频部分能量更少), 经常被用于图像处理之中. JPEG 即是利用了该性质进行图像压缩.

需要注意的是通常一维 DCT 的实现时间复杂度为 $O(N^2)$, 因此对于一维信号的分析仍较多使用 DFT.

短时傅里叶变换

对信号直接进行 DFT 可以得到整个信号各频率的强度. 然而对于实际的信号如音频信号，信号在各时间上的频率信息是不一样的. 直接对整个信号进行 DFT 则丢失了时间信息.

一个办法是将信号按照时间截取短的等长的” 帧”, 再对每帧进行 DFT, 这便是短时傅里叶变换 (STFT). 由于每帧时间较短可以假定信号在一帧之内频率信息基本一致，对于音频信号一般的共识是在 10ms-40ms 内信号基本是平稳的.

若直接对截取的信号进行 DFT 则可能因为周期延拓时的跳变导致频率泄露 , 此时需要对截取后的信号乘上一个窗函数再进行 DFT 以减小频率泄露. 一个比较常用的窗函数为汉宁窗:

\[\begin{aligned} W_{N,n}=\begin{cases} \frac{1}{2}\left(1-\cos\frac{2\pi n}{N-1}\right)&,0\leq n <N \\ 0&,{\rm otherwise} \end{cases} \end{aligned}\]

其中的 $N$ 为帧长度.

加窗后，信号 $x_n$ 在第 $t$ 帧 (从 0 开始) 的强度值 $x_{t,n}$ 则为:

\[ x_{t,n} = x_nW_{N, (n-tH)} \]

其中的 $H$ 通常称为 hop size, 即两帧之间” 越过” 的采样点数量.

对第 $t$ 帧进行 DFT, 第 $k$ 频率的强度 $X_{t,k}$ 即为:

\[ X_{t,k} = \sum_{n=0}^{N-1}x_{t,(n+tH)}w_N^{kn} \]

对于逆 STFT 则较为复杂，由于每个帧之间可能有重叠，对修改后的 STFT 每帧进行 DFT 可能每帧的重叠部分有冲突，无法对应到真实存在的信号.

其中一种想法是使用窗函数进行加权平均，但使用最多的是如下的方法:

假设有一信号 $y_i$, 对其进行 STFT 可得 $Y_t[k]$, 考虑修改后的 STFT$X^*_{t,k}$ 与 $Y_{t,k}$ 的距离的平均平方和:

\[ D(X^*,y) = \sum_t\frac{1}{N}\sum_{k=0}^{N-1}\mid X^*_{t,k} - Y_{t,k} \mid^2 \]

由 DFT 的线性性质以及帕塞瓦尔定理，则有:

\[\begin{aligned} D(X^*,y) &= \sum_t \sum_{n=0}^{N-1}( x^*_{t,(n+tH)} - y_{t,(n+tH)} )^2 \\ &= \sum_t \sum_n ( x^*_{t,n} - y_{n}W_{N,(n-tH)} )^2 \end{aligned}\]

对 $y$ 求导，等于 0 时 $D$ 为极小值，有:

\[\begin{aligned} & \sum_n\sum_t x^*_{t,n}W_{N,(n-tH)} \\ =& \sum_n y_n \sum_t W^2_{N,(n-tH)} \end{aligned}\]

对比 $\sum_n$ 各项，即有:

\[ y_n=\frac{\sum_t x^*_{t,n}W_{N,(n-tH)}}{\sum_t W^2_{N,(n-tH)}} \]

如上所述，据此重建的信号的 STFT 与原来修改得到的 STFT 的平均平方误差最小.

需要注意分母 $\sum_t W^2_{N,(n-tH)}$ 不能为 0, 因此对于以 0 开头的窗函数可能需要向前填充 0 并且保留一定的帧重叠.

由一维到二维

对于二维的信号，有二维傅里叶变换 2FT:

\[ 2FT[f](\omega, \nu) = \int_{-\infty}^{+\infty}\!\!\!\int_{-\infty}^{+\infty}f(x,y)e^{-{\rm j} (\omega x + \nu y)} {\rm d}x{\rm d}y \\ 2IFT[F](x, y) = \frac{1}{4\pi^2}\int_{-\infty}^{+\infty}\!\!\!\int_{-\infty}^{+\infty}F(\omega,\nu)e^{ {\rm j} (\omega x + \nu y)} {\rm d}\omega{\rm d}\nu \\ \]

可以发现基底 $e^{-{\rm j} (\omega x + \nu y)}$ 实际上是两个一维的傅里叶变换的乘积.

由此即可推出二维离散傅里叶变换 2DFT:

\[ X_{k,l} = \sum_{m=0}^{M-1}\sum_{n=0}^{N-1}x_{m,n}w_{M}^{km}w_N^{ln} \\ x_{m,n} = \frac{1}{MN}\sum_{k=0}^{M-1}\sum_{l=0}^{N-1}X_{m,n}w_{M}^{-km}w_N^{-ln} \\ \]

可以看出实际上可以对每行进行 DFT 后再对每列进行 DFT 即可得到二维的 2DFT. 时间复杂度即为 $O(MN\log MN)$

同样也有二维 DCT, 设 $c_{N,k,m}=\cos( \pi k(2m+1)/2N)$, $\beta_{m,n}=\alpha_m\alpha_n$:

\[ y_{k,l}=4\beta_{k,l}\sum_{m=0}^{M-1}\sum_{n=0}^{N-1}x_{m,n}c_{M,k,m}c_{N,l,n} \] \[\begin{aligned} x_{m,n} &= \frac{y_{0,0}}{4MN\beta_{0,0}} \\ & + \frac{1}{2MN}\left( \sum_{k=0}^{M-1}\sum_{kl=0,l<N}\frac{y_{k,l} }{\beta_{k,l} }c_{M,k,m}c_{N,l,n} \right) \\ & + \frac{1}{MN}\left( \sum_{k=1}^{M-1}\sum_{l=1}^{N-1}\frac{y_{k,l} }{\beta_{k,l} }c_{M,k,m}c_{N,l,n} \right) \\ \end{aligned}\]

二维 DCT 经常用于图像有关的处理，如图像压缩 (JPEG) 或图像隐水印. JPEG 即是对图像分为 $8\times 8$ 的块后对每块进行 DCT, 然后对 DCT 参数进行量化丢弃部分人眼无法辨别的高频参数后进行游程编码. 隐水印则是将水印信息嵌入人眼难以观察的中高频参数中.