(luogu1801)黑匣子

发表于 | 分类于 ，

原题链接

思路:

其实用平衡树也可以直接解决该题, 但显然写平衡树太麻烦了.

维护一个大根堆和一个小根堆. 限制大根堆的大小为所求位次, 且大根堆的元素均小于等于小根堆的元素, 此时大根堆的堆顶即为所求位次的数,

具体来讲, 每次添加一个数时先加入大根堆中, 若此时大根堆的大小大于限制的大小, 则将堆顶元素加入小根堆并弹出. 限制大小增加时优先从小根堆的堆顶中取数.

此即所谓”对顶堆”, 即两个堆的堆顶”相对”, 从中间”分开”.

大概脑补一下就像这样:

对顶堆

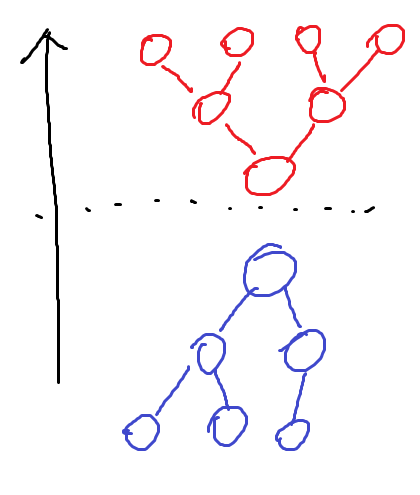
代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <cstdio>
#include <queue>
using namespace std;
const int Mn(200500),Mm(200500);
int a[Mn],u[Mn];

int main() {
    int m,n;
    scanf("%d %d",&m,&n);
    for(int i(1);i<=m;++i) {
        scanf("%d",a+i);
    }
    for(int i(1);i<=n;++i) {
        scanf("%d",u+i);
    }
    int p1(0),p2(1);
    priority_queue<int,vector<int>,greater<int> > q1;   //小根堆
    priority_queue<int> q2; //大根堆
    for(int i(1);i<=m+n;++i) {
        if(p2<=n && p1+1>u[p2]) {
            // get
            printf("%d\n",q2.top());
            if(!q1.empty()) {   //尝试从小根堆取出元素
                q2.push(q1.top());
                q1.pop();
            }
            ++p2;
        } else {
            // add
            ++p1;
            q2.push(a[p1]);
            if(q2.size()>p2) {  //将大根堆堆顶弹出到小根堆
                q1.push(q2.top());
                q2.pop();
            }
        }
    }
    return 0;
}