Pollard-Rho 因数分解

发表于 分类于 ，

随机算法玄学

概论:

Pollard-Rho 算法是一个启发式算法，它解决的是这样一个问题: 对于一个合数 \(n \in N^*\), 快速找出它的一个因数.

最简单能想到的办法是试除法，即在 \([2,\sqrt{n}]\) 上寻找能整除 \(n\) 的数，时间复杂度是 \(O(\sqrt{n})\).

但若 \(n\) 一旦较大 \(O(\sqrt{n})\) 的复杂度就会显得不太够用. 这个时候可以发挥猴子排序的思想，直接在 \([1,n]\) 中猜一个数，最优时间复杂度便是 \(O(1)\). 但这个方法显然准确率太低.

生日悖论与随机:

生日悖论指的是这样一个问题：房间里有 23 个人， 那么其中有两个人生日相同的概率是多少？

通过计算可知，概率为 \(P = \frac{365!}{365^{23} \times 342!} \approx 0.4927\), 大致是 1/2!

生日悖论的实质是：满足答案的组合比单个个体要多， 所以采用组合的方式随机要比单个随机准确率更高.

受到该” 悖论” 启发，一个随机数不行我们可以取两个随机数，例如：在 \([1,1000]\) 中随机取一个数， 取到 23 的概率是 1/1000, 但在 \([1,1000]\) 中随机取两个数 \(i,j\), 其差的绝对值 \(|i-j|\) 等于 23 的概率大约是 0.195%, 大约提升了一倍.

概率优化:

虽然通过取两个随机数提升了准确率。但是提升一倍还是不够的.

一个重要的想法是：两个数的最大公约数一定是某个数的因数。也就是说， 我们随机一个数 \(k\), 只要 \(gcd(k,n) > 1\), 则可以求得一个因数 \(gcd(k,n)\). 这样的 k 有很多: n 有很多因子， 每个因子的倍数都可以作为合适的 k.

将两个优化合起来：选取两个随机数 \(i,j\), 若有 \(gcd(|i-j|,n)>1\), 则找到一个 \(n\) 的因子 \(gcd(|i-j|,n)\). 这便是 Pollard-Rho 算法的核心.

随机算法优化:

直接用 C 自带的随机数实现上述思想会发现运行很慢. Pollard 的原版中给出了一个函数 \(g(x) = (x^2 - 1) mod\ n\), 使用这个函数迭代来生成一个伪随机序列，即 \(x_i = g(x_{i-1})\).

由于 \(mod\ n\) 的存在， 序列中最多出现 n 个数。所以这个伪随机序列中一定会存在一个环， 画出来就像这个样子: (图片来自维基)

Rho

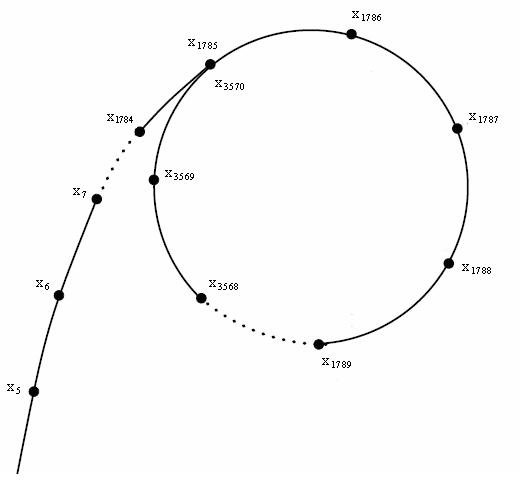
看起来像希腊字母 \(\rho\)(rho), 所以该算法叫 Pollard-Rho (233).

为了避免在环上递推过多，使用 Floyd 判环算法，即使用两个变量 \(x,y\), 从同一起点开始， 用类似” 龟兔赛跑” 的方式，x 每次往后迭代一次，y 每次往后迭代两次， 迭代后以 x,y 作为判定数判定，当两个数相等时说明” 兔” 已经领先” 龟” 一圈， 结束迭代，返回判定失败，使用其他初始值重新判定.

实际运用中可能伪随机生成序列中找不到合适的 k, 一个例子是 4. 这个时候可能需要更改生成伪随机序列的递推方程. 其中一种选择是将原来的 \(g(x)\) 拓展到 \(g(x) = (x^2 + c)mod\ n\), 并随机选取常数 c 重新启动过程.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
typedef long long LL;
LL g(LL x,LL c,LL n) {
    return ((__int128)x*(__int128)x+c)%n;
}
LL pR(LL x) {
    LL c=rand()%(x-1)+1;
    LL p1 = g(0,c,x), p2 = g(g(0,c,x),c,x); //"龟兔"流程
    while(p1!=p2) {
        LL d = gcd(abs(p2-p1),x);
        if(d > 1) { //找到一个因数便返回
            return d;   
        }
        p1 = g(p1,c,x), p2 = g(g(p2,c,x),c,x);  //递归
    }
    return x;   //没有找到
}

其他优化:

可以使用一个叫做 Brent 判环算法来加速算法 (维基上是说平均能提升 24%), 具体过程类似于 Floyd 判环，但是每次后一个变量比前一个变量多递推 \(2^s\) 次，其中 s 是一个变量，从 0 开始， 每次递推完成后将后一个变量的值保存到前一个变量并 s 自增 1.

同时注意到算法中需要多次计算 gcd, 而 gcd 的时间复杂度为 \(O(logn)\), 可以通过减少 gcd 的计算次数来达到较大的常数级优化:

注意到如果 \(gcd(a,n)>1\), 那么显然对于任意的正整数 \(b\), 有 \(gcd(ab,n)>1\). 同时根据欧几里得算法， 有 \(gcd(ab,n) = gcd(ab\ mod\ n,n)\).

我们可以每次取得一个 \(|i-j|\), 不直接去计算 \(gcd(|i-j|,n)\), 而是累乘到一个数 \(z\) 中， 累乘到一定次数后再去计算 \(gcd(z,n)\).

累乘次数的选取很重要，少了效果不佳， 多了累乘过头没有判定也可能效果不佳. 同时可能导致累乘到同一因数过多而导致一直取到平凡因数 n 而导致算法失败. 一个解决方法是在判定到 z = 0 时回退并重新累乘.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
LL pR(LL x) {
    LL c=Rand()%(x-1)+1;
    LL s(0),t(0);
    LL val(1);  //累乘数
    for(int k(1);;k<<=1) {  //Brent判环
        s = t;
        val = 1;
        for(int i(1);i<=k;++i) {
            t = g(t,c,x);
            if(t==s) {  //判定到环返回失败
                return x;
            }
            LL tmp = (__int128)val*abs(t-s)%x;
            if(tmp == 0) {  //累乘过多回退
                break;
            }
            val = tmp;
            if(i%127==0) {  //累乘上限
                LL d = gcd(val,x);
                if(d>1) {
                    return d;
                }
                val = 1;
            }
        }
        LL d=gcd(val,x);
        if(d>1) {
            return d;
        }
    }
    return x;
}