Johnson 全源最短路

发表于 分类于 ，

概述:

最为熟知的全源最短路算法肯定是 floyd, 时间复杂度是 \(O(n^3)\).

但是当给出的图是稀疏图，边权为非负值时，可以直接跑 n 遍 dijkstra, 时间复杂度是 \(O(nmlogn)\), 此时 m (边数) 与 n (点数) 同阶，要比 floyd 更优.

但 dijkstra 不能正确求解带负权边的最短路， 对于带负权边的图我们需要经过预处理，使得所有的边权非负. 这便是 Johnson 算法要做的.

实现:

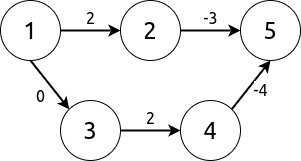
Johnson 算法引入了一个物理概念–势能。将图 G 中点 \(i\) 的” 势能” 记为 \(h_i\).

G

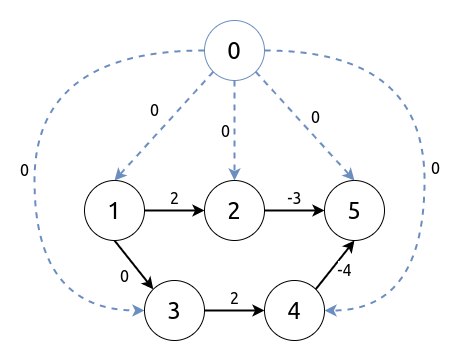
为了求得 \(h_i\), 首先新建一个虚拟节点 (设其编号为 0).

G

接下来用 Bellman-Ford (spfa) 求出 0 号节点到各点的最短路，即为 \(h_i\).

G

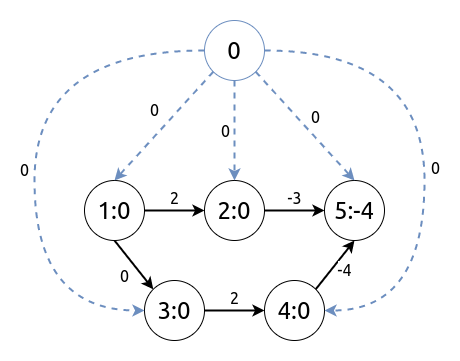
对于原图 G 中的某条边 \(\langle u,v \rangle\), 重新设置它的边权为 \(w \langle u,v \rangle -(h_v-h_u)\).

G’

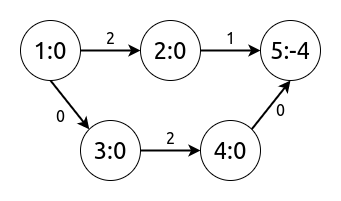
接下来遍历起点，跑 n 遍 dijkstra 即可.

时间复杂度为 \(O(nm+nmlogn)\)

正确性证明:

需要证明的是两个命题，即重构后的图上的最短路径和原图的最短路径一致， 以及重构后每条边的边权均为非负值.

证明 1/2:

重构后的图中，从 \(s\) 到 \(t\) 的一条路径 \(s \to p_1 \to p_2 \to \cdots \to p_k \to t\) 的长度为:

从这里可以看出” 势能” 这个名字的由来：无论走哪条路径，最后的 \(h_t-h_s\) 是不变的.

同时由于 \(h_t-h_s\) 是定值， 前面的部分为原图的路径长度， 因此重构后图上的每条路径都与原图相对应

证明 2/2:

根据预处理 (Bellman-Ford 或 spfa) 以及三角形不等式，对边 \(\langle u,v \rangle\), 有不等式 \(h_v \le h_u + w \langle u,v \rangle\).

移项即得 \(w' \langle u,v \rangle = w \langle u,v \rangle -h_v+h_u \ge 0\), 即重构后的图边权均非负. 证毕.

代码:

(luogu5905) Johnson 全源最短路模板 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int Mn(3050),Mm(10050);

//建图
int n,m;
struct edge
{
    int e,v,nt;
}ed[Mm];
int vs[Mn],ec(0);
void adde(int u,int v,int w)
{
    ed[++ec] = (edge){v,w,vs[u]};
    vs[u] = ec;
}

//求h
int h[Mn],inq[Mn];
bool isq[Mn];
bool spfa(int s)
{
    fill(h,h+Mn,static_cast<int>(1e9));
    queue<int> q;
    h[s] = 0; ++inq[s];
    q.push(s);
    while(!q.empty())
    {
        int xn(q.front()); q.pop();
        isq[xn] = false;
        if(inq[xn]>=n)  return false;
        for(int i(vs[xn]);i;i=ed[i].nt)
        {
            edge& e(ed[i]);
            if(h[e.e]>h[xn]+e.v)
            {
                h[e.e] = h[xn] + e.v;
                if(!isq[e.e])
                {
                    q.push(e.e);
                    isq[e.e] = true; ++inq[e.e];
                }
            }
        }
    }
    return true;
}

//堆优化dijkstra
struct qn
{
    int n,d;
    bool operator <(const qn& rhs) const    //小根堆
    { return d>rhs.d; }
};
int d[Mn];
bool isd[Mn];
void dij(int s)
{
    fill(d+1,d+n+2,static_cast<int>(1e9));
    memset(isd,0,sizeof isd);
    priority_queue<qn> pq;
    d[s] = 0;
    pq.push((qn){s,0});
    while(!pq.empty())
    {
        qn x(pq.top()); pq.pop();
        if(isd[x.n]) continue;
        isd[x.n] = true;
        for(int i(vs[x.n]);i;i=ed[i].nt)
        {
            edge& e(ed[i]);
            if(d[e.e]>d[x.n]+e.v-h[e.e]+h[x.n])
            {
                d[e.e] = d[x.n]+e.v-h[e.e]+h[x.n];
                pq.push((qn){e.e,d[e.e]});
            }
        }
    }
}

int main() {
    scanf("%d %d",&n,&m);
    for(int i(1);i<=m;++i)
    {
        int u,v,w;
        scanf("%d %d %d",&u,&v,&w);
        adde(u,v,w);
    }
    for(int i(1);i<=n;++i)    //添加虚拟节点(这里编号是n+1)
        adde(n+1,i,0);
    if(!spfa(n+1))    //如果有负环
    {
        printf("-1");
        return 0;
    }
    for(int i(1);i<=n;++i)
    {
        long long ans(0);
        dij(i);
        for(int j(1);j<=n;++j)
        {
            if(d[j]!=1e9)   ans += 1ll*j*(d[j]+h[j]-h[i]);    //注意d[j]和原图最短路有区别
            else            ans += 1ll*j*d[j];
        }
        printf("%lld\n",ans);
    }
    return 0;
}