(POJ1860) Currency Exchange

发表于 分类于 ， ，

(今天训练赛的题，回寝把思路理了一下把代码写出来了)

思路:

spfa 判负环

以货币类型建图

从 S 开始，如果能找到一个环， 使得从沿着这个环兑换一轮后货币量增加了 (即注释所谓” 增环”(自造词)), 则说明可以倒获得利益

(类似于判负环但其实不是负环)

下面给个简单证明:

假设某个” 增环” 中有三个结点:

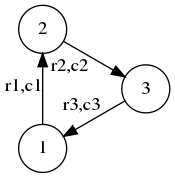
3_cycle

假设 1 开始时为 x 个货币，沿环一圈后货币量为:

$    ( ( r_{1} x - r_{1} c_{1} ) r_{2} - r_{2} c_{2} ) r_{3} - r_{3} c_{3} $

$ =r_{1} r_{2} r_{3}x - ( r_{1} r_{2} r_{3} c_{1} + r_{2} r_{3} c_{2} + r_{3} c_{3} ) $

$ > x $

括号内为常量且大于 0, 所以:

$ r_{1} r_{2} r_{3} x > x      r_{1} r_{2} r_{3} > 1 $

由函数相关知识可知，对于更大的 x, 上述不等式依然成立， 且可递推到无限 (不知道咋证，但应该是对的……(小声))

同时可推广结点数更大的环.

且可由 S 到该环，则由题意，必然可从该环到 S, 且必然存在存在一个循环次数， 从该环循环该次数后，回到 S 货币增加.

同时显然地， 至少应该存在一个包含 S 点的” 增环” 才能使得货币增加 (从 S 到” 增环” 再回到 S 可看作是复用某些结点的” 增环”).

证 (luan) 明 (che) 完后就是代码:

代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <cstdio>
#include <queue>
using namespace std;
const int Mn(105),Mm(105);
/*------建图, 前向星------*/
struct edge
{
    int e,nt;
    double r,c;
}ed[Mm<<1];
int vs[Mn],ec(0);
void adde(int s,int e,double r,double c) //加边
{
    ed[++ec] = (edge){e,vs[s],r,c};
    vs[s] = ec;
}
/*------spfa有关------*/
double d[Mn]; //距离(即该种货币所能得到的最大数量)
int qcnt[Mn]; //计数器, 计算入队次数
bool isiq[Mn]; //判定是否在队列中

int main()
{
    int n,m,S;
    double v;
    /*------输入------*/
    scanf("%d %d %d %lf",&n,&m,&S,&v);
    for(int i(1);i<=m;++i)
    {
        int a,b;
        double r1,c1,r2,c2;
        scanf("%d %d %lf %lf %lf %lf",&a,&b,&r1,&c1,&r2,&c2);
        adde(a,b,r1,c1);
        adde(b,a,r2,c2);
    }
    /*------spfa------*/
    queue<int> q;
    q.push(S);
    d[S] = v;
    bool ans(false);
    while(!q.empty())
    {
        int x(q.front()); q.pop();
        isiq[x] = false; //出队清除标记
        if(qcnt[x]==n)	//如果有"增环"(自造词)
        { ans=true; break; }
        for(int i(vs[x]);i;i=ed[i].nt)
        {
            edge& e(ed[i]);
            if((d[x]-e.c)*e.r>d[e.e]) //松弛
            {
                d[e.e] = (d[x]-e.c)*e.r;
                if(!isiq[e.e]) //如果不在队列则入队
                {
                    isiq[e.e] = true;
                    q.push(e.e);
                    ++qcnt[e.e];
                }
            }
        }
    }
    if(ans)	printf("YES\n");
    else	printf("NO\n");
    return 0;
}