思路:
用一个二维数组存储下每个位置之前的所有的颜色的客栈个数 (即前缀和),
并记录下每一个在限制范围内的客栈
以这些客栈为分割点,将整个区间分为若干段 (不包括分割点)
对于每个分割点,统计它之前的区间与后面的一段的方案数,
对分割点单独统计,这样便可以做到不重复也不遗漏统计
以下图作为例子 (第二行为编号,第三行为颜色,第四行为费用): ![luogu1311_sample]() 其中,
2,5,7 为限制范围内的客栈,将客栈分为 1~1,3~4,6~6,8~8 四段
其中,
2,5,7 为限制范围内的客栈,将客栈分为 1~1,3~4,6~6,8~8 四段
对第一个分割点 2, 讨论 1~4. 若不选 2, 有 1 种方案;若选 2, 有 1 种方案
对第二个分割点 5, 讨论 1~6. 若不选 5, 有 2 种方案;若选 5, 有 3 种方案
对第三个分割点 7, 讨论 1~8. 若不选 7, 有 4 种方案;若选 7, 有 2 种方案
所以答案为 13
下面是代码
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
| #include <iostream>
#include <cstdio>
#include <vector>
#include <cstring>
using namespace std;
const int Mn(200050);
int hn[Mn][55];
vector<int> pp;
vector<int> pc;
int main()
{
int n,k,p;
scanf("%d%d%d",&n,&k,&p);
for(int i(1);i<=n;++i)
{
int clr,cst;
scanf("%d%d",&clr,&cst);
if(cst<=p) { pp.push_back(i); pc.push_back(clr); }
memcpy(hn[i],hn[i-1],sizeof hn[i]);
++hn[i][clr];
}
int ans(0);
for(int i(0);i<pp.size()-1;++i)
{
for(int j(0);j<k;++j)
ans += hn[pp[i]-1][j] * (hn[pp[i+1]-1][j]-hn[pp[i]][j]);
ans += hn[pp[i+1]-1][pc[i]]-1;
}
for(int j(0);j<k;++j)
ans += hn[pp[pp.size()-1]-1][j] * (hn[n][j] - hn[pp[pp.size()-1]][j]);
ans += hn[n][pc[pc.size()-1]]-1;
cout << ans;
return 0;
}
|
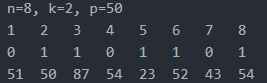 其中,
2,5,7 为限制范围内的客栈,将客栈分为 1~1,3~4,6~6,8~8 四段
其中,
2,5,7 为限制范围内的客栈,将客栈分为 1~1,3~4,6~6,8~8 四段