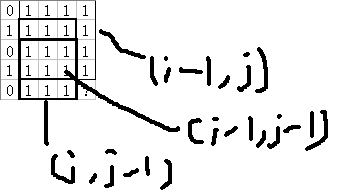(luogu2701) 巨大的牛棚 (USACO5.3)

发表于 分类于 ，

最大正方形

又一个 dp 的模板 ## 题目描述:

在 n*n (n<=1000) 的矩阵中，有几个点不能选， 找出当中边长最大的正方形

思路:

设 d (i,j) 是以点 (i,j) 为右下角的最大正方形边长

则有 d (i,j) = min {d (i-1,j),d (i,j-1),d (i-1,j-1))+1

即只有当上面，左边，左上角都能构成边长为 k 的正方形时， 点 (i,j) 才能形成边长为 k+1 的正方形

代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
nclude <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int Mn(1005);
bool mp[Mn][Mn];
int d[Mn][Mn];
int main()
{
    int n,t;
    cin >> n >> t;
    memset(mp,-1,sizeof mp);
    for(int i(0);i<=n+1;++i)
        mp[0][i] = mp[n+1][i] = mp[i][0] = mp[i][n+1] = false; //处理边界
    while(t--)
    {
        int x,y;
        scanf("%d %d",&x,&y);
        mp[x][y] = false;
    }
    int Max(0);
    for(int i(1);i<=n;++i)
        for(int j(1);j<=n;++j)
            if(mp[i][j])	
            {
                d[i][j] = min(min(d[i-1][j],d[i][j-1]),d[i-1][j-1])+1;
                Max = max(Max,d[i][j]);
            }
    cout << Max;
    return 0;
}